When to use Barnes-Hut simulation
I implemented n-body simulation first with naive approach using vector as a basis for storage and iteration, and then again with Barnes-Hut simulation (BH from now on) using QuadTree. I only expected to need something like 100 bodies in my program and I wondered wether BH is faster in that region of problem size or not quite yet. The vector has an advantage of being cache friendly, but BH is better asymptotically. Where is the tipping point, if you use sane values for theta?
I think I have created at least somewhat performant BH by iteratively running Valgrind and making improvements, so it should be realistic BH to compare to. For tests, I created two equal sized spaces, scattered a selected number of bodies with random velocities into both systems equaly, so that both systems had equal copies of setup, ran one step of gravity simulation, and measured time to complete. Note that this is the worst case for BH, because BH really starts to shine when leveraging distributions of bodies that are more grouped together. All calculations were done on a single thread on Intel(R) Core(TM) i5-2450M CPU @ 2.50GHz, with 3MB cache, running openSUSE 13.2.
Results
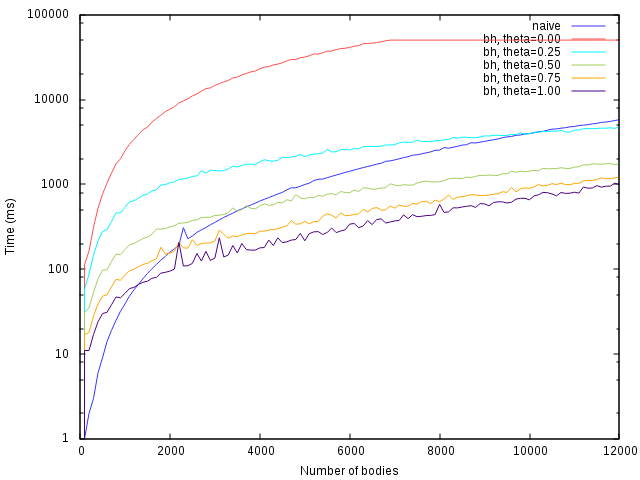
The table below shows numbers of bodies where straightforward vector implementation reliably stops being more efficient compared to equivalent BH solution configured with given theta value setting.
| theta | number of bodies |
|---|---|
| 1.00 | 1500 |
| 0.75 | 2500 |
| 0.50 | 4000 |
| 0.25 | 10500 |
But as usually happens in software, it is not all that simple. There is more bad news for vector. Whenever I ran gravity simulations for a couple of steps I observed strange, almost random variations in execution times, where it would either complete fairly quickly as in the charts above or something would go terribly wrong and it would for some reason complete 100 times slower then expected for that problem size. It was as it were two different implementations running. These are the results from running 10 steps of gravity simulation on vector implementation only:
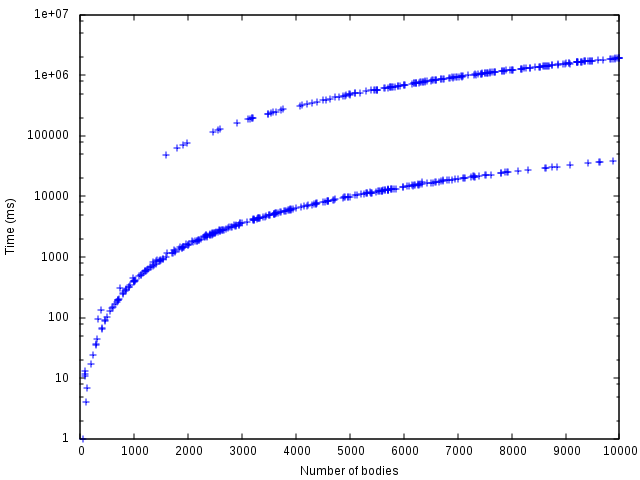
Why does performance of vector based implementation vary so much? I ran tests on my CPU with two cores, each of which has two threads that share cache. I suspected that there was some sort of cache thrashing happening because of some other processes in the system. I rebooted into runlevel 1, isolated the whole core of CPU using cpusets in order to dedicate it to this process only, decreased niceness, and set priority to realtime. L3 cache was still shared between cores, but if I fence off the two hardware threads that share L1 and L2, the improvement should be significant for up to about 4000 items. That number of items of 60 bytes should fit into 256KB of L2 and avoid much of the thrashing. I did all that and noticed no improvement. I could not fence off kernel threads like kworker and migration and such, but this is kinda hard when you are not running real-time operating system, not to mention it is really impractical.
At the moment I have no other ideas what it could be. But I digress. So many interesting things to explore, so little free time!
Conclusion
For body count less then 1500, don't bother with Barnes-Hut. For body counts larger then about 4000, don't bother with vector, despite measurements showing it might be faster.
Previous:
Improvement to three-way min
Next:
Peformance implications of compacting vector elements