Matej++

Peformance implications of compacting vector elements

I stumbled on this particular performance improvement more or less by accident when I was doing profiling for my quadtree-based n-body simulation.

Consider the following situation. There is a vector of elements with numerous fields. You need to iterate the vector many times, but only need a subset of elements' fields. Now, every time you touch an element of the vector, even if it is just to read one of the fields, the whole memory block will be pulled into cache. The next element's field will perhaps be in the cache, but it will be far away, because all unneeded fields will lie between them. In this case you can create another vector that will contain elements that only contain necessary fields. Then you can copy needed values from the vector of bigger elements to the vector of smaller elements. More smaller elements will fit onto a cache line than larger elements. All data pulled into cache will be accessed, there is no waste in terms of cache space. Price to pay is that one time memory allocation and copying operation before iteration begins.

Is it worth it? And if so, when?

Measurements

As usual, all measurements were only done on my home PC, on a single thread, on Intel(R) Core(TM) i5-2450M CPU @ 2.50GHz, with 3MB cache, running openSUSE 13.2.

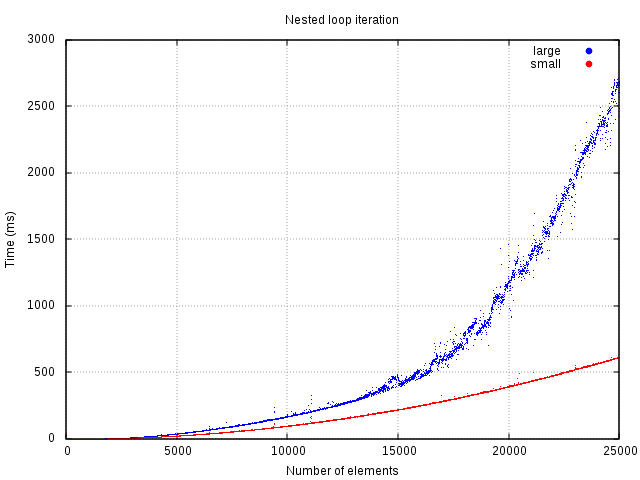
I created two structs, one with 20 fields of type double, and one with only 2 such fields. A 90% reduction. I then first iterated the vector with large structs and then again an equal vector of small structs in multiple ways: a limited number of start to end iterations (count * linear), nested loop iterations (quadratic), and simply accessing random element many times (constant * linear).

struct large_element {
   double fields[20];
};
struct small_element {
   double fields[2];
};

The performance gain shows most prominently on nested loop iteration.

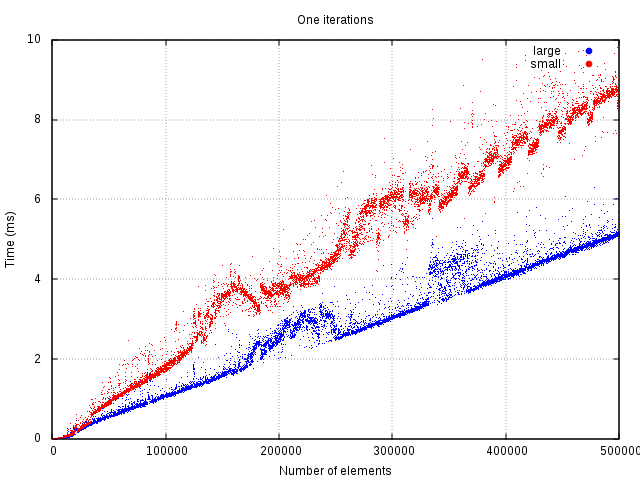
Theoretically, there should be no performance gains when only doing one iteration. The reason for this is that copying part itself is an iteration and could be used to just get to the point instead. The measurements support this expectation.

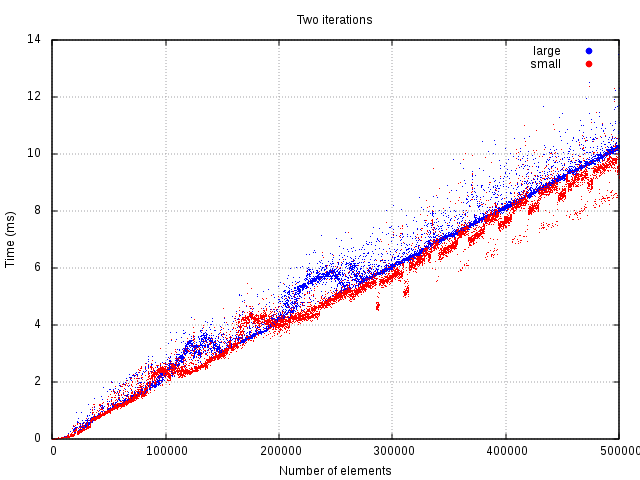
At least two iterations need to be done for the initial price of copying to be canceled out by the gains of faster iteration. Three iterations or more, the copying is already paid off and iteration can be done measurably faster.

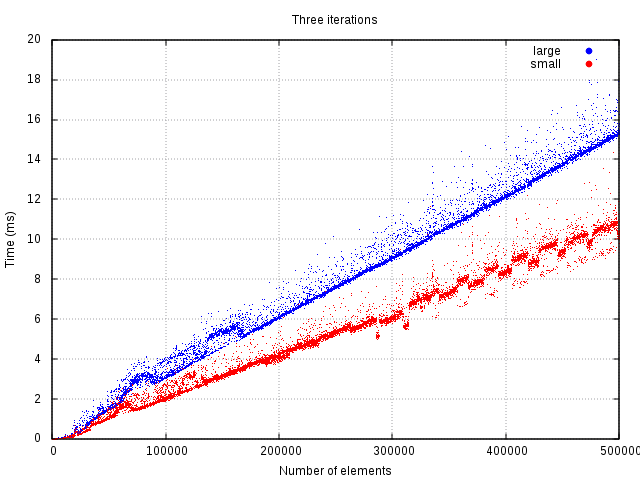
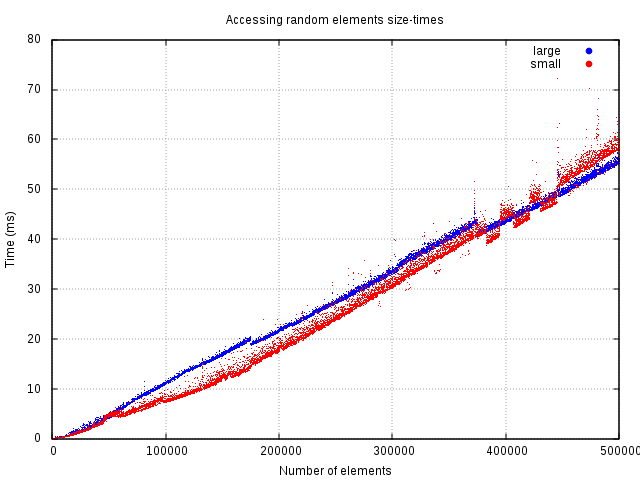
If a random element's fields need to be selected from vector a many times, it is more likely that the information will reside in the cache already if more items fit in there. That can explain measurable performance gains in random selection. It was done by selecting random element from the vector as many times, as there were elements in the vector. It shows that in this setup, it is equally quick to randomly select from bigger or smaller vector. Anything more than that will show performance improvement.

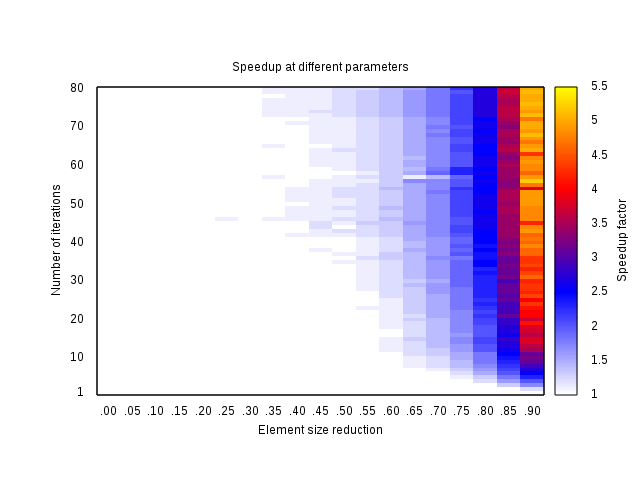
All experiments were done with 90% reduction in element size and a handful of different iteration schemes. Here are measurements of different reductions with different number of iterations. Tests were done on a vector of 500.000 elements, to bring out the difference. Large element size remained 20 doubles, which were reduced when copying into smaller elements of sizes between 20 and 2, to give increasing reduction.

Graph of constant number of iterations shows this improvement doesn't really work unless you can reduce your data by at least 50%, but in order to make the effort worthwhile, it should be more than 75%. Also, it seems, that although performance gains grow with increased iterations count, the speedup is primarily a function of reduction. For example: 85% reduction did not improve performance beyond factor 4, be it at 20 iterations or 80. Likewise, 90% reduction speedup was upward limited at 5.5.

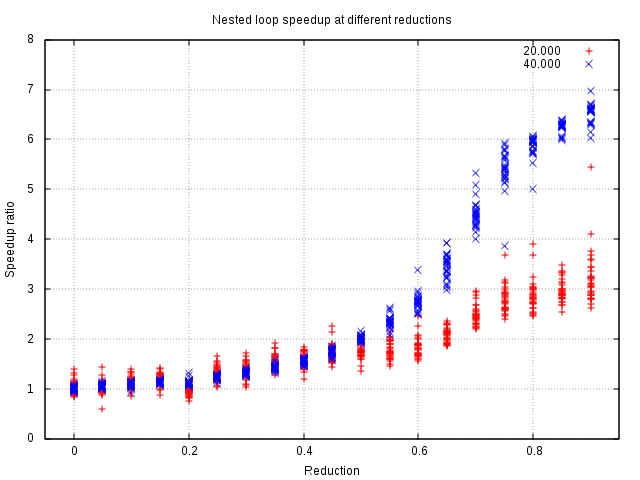
Similar observation can be done for nested loops too, appart from the fact that the performance improvement is heavily dependent on size of a vector in question, exactly because it is a quadratic function. Still, there is distinct requirement that the reduction is at least 50%, otherwise it's probably not worth the trouble, if you don't really need that fractional improvement. Although on the other hand you could argue that it is no worse, so worth it in any case; I guess it depends on the task at hand, as always.

Applicability

This trick can be successfuly used in vectors where the data itself is stored, not where the pointers to data are stored. When you need to dereference a pointer and load the data from memory in separate step, you thrashed the cache already. Unfortunately in practice, vectors are often used to store pointers, in which case this optimisation is not an option. Worse even, the optimisation has most impact when the elements stored are big compared to parts of them that need to be iterated, which are exactly the cases where programmers choose to store pointers instead.

An additional argument why when programming, you should be mindful about data locality.

Full listing of testing code is too boring for blog, but if you'd like to see it anyway, see the page source.

Previous: When to use Barnes-Hut simulation
Next: When to use nested namespaces in C++