Matej++

Solving Sudoku with A*

A* algorithm is used for searching shortest paths, but is widely being adapted to search solutions for puzzles, that can be represented in form of the graph. Puzzles for which it is suitable the most are ones that do not have a very big number of possible next moves, like for instance 15-puzzle. Despite the fact that Sudoku is different in that sense, it has been attempted before [ pdf ] and it was successful.

There are two possible outputs to solving Sudoku: the solution of the puzzle or a note, that puzzle is unsolvable. A* will correctly calculate the solution if it exists because eventually it will check each possible puzzle. The real question is therefore not whether it can come to correct solution, but rather if it can to do that in timely manner. Also, time is not the only limitation. With all possible intermediate steps that must be stored in memory, the available memory space is an obstacle, at which A* can fail.

I implemented everything in C#. For A* to work, I needed minheap, which is to my big surprise absent from .NET framework. Every serious programming framework should at least have a non-naive implementation of priority queue under its belt. That's no problem. I needed minheap and I implemented it. While I was at it I made maxheap and pushed it a step further and made midheap(!) Not joking, for more on this, see my other post: C# Implementations of Binary Heaps .

Now I could start assembling parts. I randomly generated a puzzle. This was done by storing 81 numbers in an array. Each number from 1..9 was repeated 9 times. Then I removed from the array ones that were given to solver as a base problem. The rest I shuffled by Fisher-Yates, that is also part of my Blitva library , if anyone needs it. After that, the numbers were prepared to fill the first random attempt as a solution.

The random solution candidate at this point has all correct numbers, but they are in wrong positions. For every number that is in wrong position, there is another that should be there, which means that pair is on wrong position also. That is the conclusion that led me to the idea how to calculate next possible generation of solutions for my A*: all possible switches of positions of two numbers, where none of them has been given as a problem (those obviously must remain in place). If only one number is given, this generates approximately 80 * 79 / 2, which is more than 3000 problems in next generation.

Function that generates all possible number switches in the puzzle:

public void createSubproblems( Sudoku bestSoFar )
{
  // for each field
  for( int i = 0; i < Settings.SudokuDimension; i++ )
  for (int j = 0; j < Settings.SudokuDimension; j++)
  // for each another field
  for( int k = i+1; k < Settings.SudokuDimension; k++ )
  for (int l = j+1; l < Settings.SudokuDimension; l++)
  // if none of the fields are fixed
  if (fixedBasis.getBox(i, j) == 0 &&
      fixedBasis.getBox(k, l) == 0)
  // switch them and create new subproblem sudoku
  {
     Sudoku newSubproblem = new Sudoku(bestSoFar);
     newSubproblem.PathLength = bestSoFar.PathLength + 1;
     // switch two values
     short temp = newSubproblem.getBox(i, j);
     newSubproblem.setBox(i, j, newSubproblem.getBox(k, l));
     newSubproblem.setBox(k, l, temp);
     // insert into minheap
     minHeap.insertItem(newSubproblem);
  }
}

Objective function was simple. Each number repeated in single line gets 1 penalty point. Each number repeat in row gets 1 penalty point. Also, each number repeated in a square gets one penalty point. I didn't have to check for occurrence of too many or too little of each number because of the way the first candidate solution was generated and how all subsequent generations of candidates are generated. In essence, a definition of Sudoku solution is used as an objective function.

Code snippet of two functions, that make an objective function, that scores given Sudoku puzzle. The largest part of code is to check each square. Writing the code to handle variable sizes of Sudoku seems, in retrospect, irrational even to me. Also, square boundaries could be calculated in advance and that would speed up the objective function, if anyone cares enough to make this silly program run faster.

private int getFieldScore(int i, int j)
{
  int fieldScore = 0;
  for( int k = 0; k < 9; k++ )
  {
    if( ( k != i && m_boxes[k,j] == m_boxes[i,j] ) ||
        ( k != j && m_boxes[i,k] == m_boxes[i,j] ) )
      ++fieldScore;
  }
  int sq_dim = Settings.SudokuDimension / 3;
  int row = i / sq_dim;
  int col = j / sq_dim;
  int row_from, row_to, col_from, col_to;
  row_from = row*sq_dim;
  row_to = row_from + sq_dim - 1;
  col_from = col*sq_dim;
  col_to = col_from + sq_dim - 1;
  for( int k = row_from; k <= row_to; k++ )
  for ( int l = col_from; l <= col_to; l++ )
    if( k != i && l != j && m_boxes[k, l] == m_boxes[i, j])
      ++fieldScore;
  return fieldScore;
}

private void calculateScore()
{
  // score consists of the sum of how wrong a number on each field is.
  // "Wrongness" is calculated by how many times the number on the field
  // appears in each line, column, square
  m_score = m_pathLength;
  for( int i = 0; i < 9; i++ )
  for (int j = 0; j < 9; j++)
  {
    m_score += getFieldScore(i, j);
  }
  m_scoreCalculated = true;
}

Each candidate solution is then stored into minheap based on it's score. A* also included path length that was "traveled" to reach a particular candidate solution. That seemed irrelevant in my case, so I omitted it at first. After that, the algorithm was just endlessly exploring all thousands of candidates that had the same score, rarely making any progress. After including path length to score criteria it noticeably sped up the process. Why is that so is beyond me. I cannot visualize how that information could help, not in general A* algorithm, but in my concrete example of solving Sudoku. Judging from particular solution candidate, how can it be important how many steps were needed to come here? It might as well be guessed at initial solution attempt, so how does it matter? Well, the measured fact is that it does.

A* part of the experiment.

public Sudoku solve()
{
  while ( (minHeap.getMin().Score - minHeap.getMin().PathLength) != 0)
  {
    Sudoku bestSoFar = minHeap.extractMin();
    createSubproblems(bestSoFar);
  }
  return minHeap.getMin();
}

Results

It works!

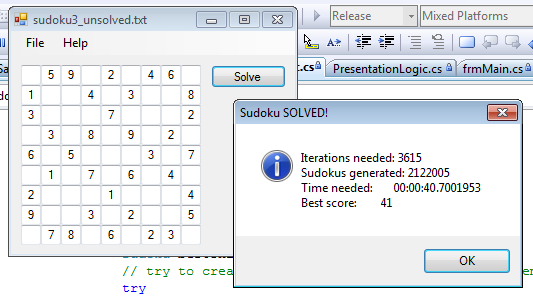
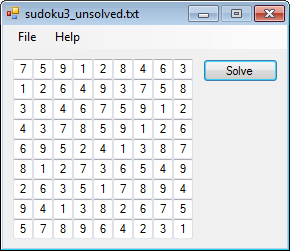
Except when it doesn't.

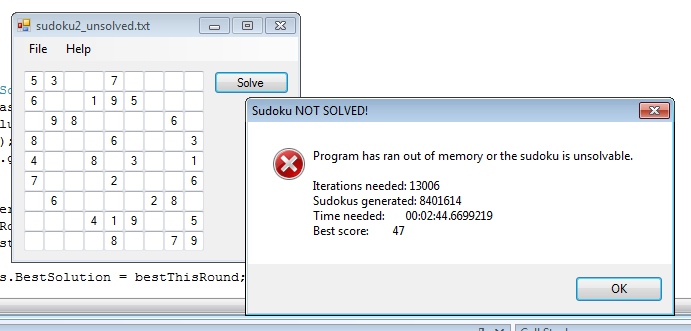
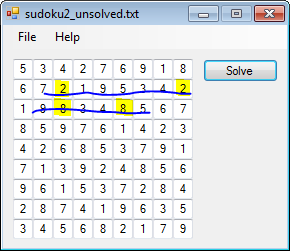
It was, of course, not unsolvable.

The memory limitation turned out to be a major issue. For every generation there are roughly 3000 problems, and only one of them gets removed as a base for generating next generation of candidates. I condensed the memory footprint of each Sudoku as much as I could without significantly complicating the program. I stored complete Sudoku in two-dimensional array of bytes, with only two integers included for current path length and score of that particular solution candidate. I stored an array of given numbers elsewhere, so that it is not repeated within every candidate. Still, each generation takes ~300k of memory. Repeat that for a couple of thousands of generations and the memory gets full. True, I built the test application 32-bit (why is that default for C# projects in VS 2008?) and I didn't feel like building it again for 64-bit, which means I could only access limited amount of RAM, but the problems remains.

Conclusion

A* is slow and very memory intensive when it is implemented the way I did it. The main problem was generating next generation of candidates. When using A* one should carefully select how many candidates will be in next generation. Few thousand is too much. Sometimes it did reach a solution with given time and mostly memory and so it was demonstrated it can work, but it is unpractical.

Alternative

Having done A* I also tried backtracking approach. This time I wrote it in C++. The results were amazing, it just spit out the solution. What I thought would be a slower process was an immensely faster way. I implemented that one using recursion. In one vector I kept all possible numbers from 1..9. Then I iterated through all the numbers and all Sudoku cells at the same time, checking at each step whether the puzzle is valid or not and backtracking if algorithm ran out of numbers from vector.

CPlainSudoku::CPlainSudoku() :
  m_numbers({1,2,3,4,5,6,7,8,9})
{
}
void CPlainSudoku::solve()
{
  std::vector<CSudokuCell>::iterator start = m_puzzle.begin();
  if(start->given)
    start = getNext(m_puzzle.begin());
  solve(start);
}
void CPlainSudoku::solve(std::vector<CSudokuCell>::iterator curr)
{
  vector<short>::iterator numbersIterator = m_numbers.begin();
  if(curr == m_puzzle.end())
  {
    m_solved = true;
  }
  else
  {
    while(numbersIterator != m_numbers.end() && !m_solved)
    {
      curr->val = *numbersIterator;
      if(valid(curr))
      {
        vector<CSudokuCell>::iterator next = getNext(curr);
        solve(next);
      }
      ++numbersIterator;
    }
    if(!m_solved) curr->val = 0;
  }
}

Previous: Cosmic ray threat?
Next: How to use member function as a callback from another class