Reversing graphs in Kosaraju's algorithm is in fact necessary
Kosaraju's algorithm for finding strongly connected components requires you to reverse graph, calculate finishing times, reverse the graph again (if you don't want to hold two different graph structures in memory) and then follow finishing times in reverse order. From unvisited node with biggest finishing time, to the unvisited node with smallest finishing time.
This double reversing, so that you can read finishing times from biggest to smallest, seems a bit redundant at first. Couldn't I just calculate finishing times on a graph as it is, then follow them in order from smallest to the biggest? Intuition tells me it should work. I wrote it and tested it and it doesn't work. Even worse, it works sometimes, so that you can, if not careful enough, easily get distracted into thinking it's ok to do so.
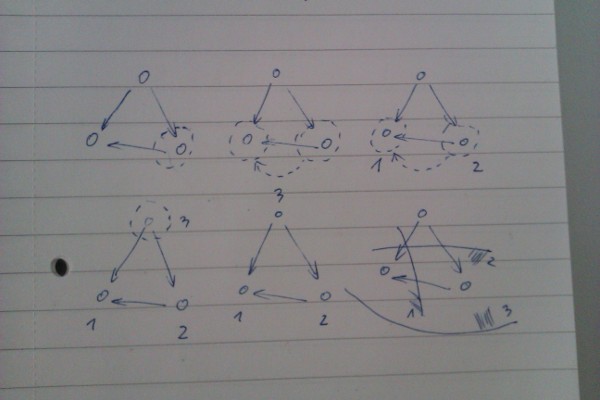
I'm not such a good theorist to prove formally that something works or not and why, but this is easier. For disproving an algorithm I must only find one case where it doesn't work and I can already claim that to be proof. So I resorted to drawing. Graph picture below represent meta-graphs; each node represents single SCC.
The first cartoon shows an example of a graph for which Kosaraju idea works even without reversing:
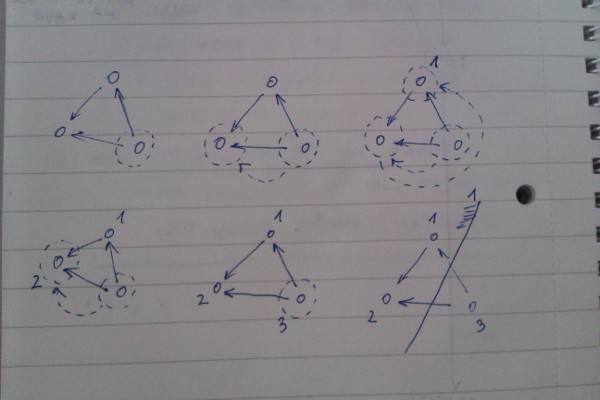
The second cartoon shows a slight modification to the graph, or the order in which nodes are visited, depends how you look at it. This change makes the modified Kosaraju come to wrong conclusion about strongly connected components: when starting from node labeled 1, it will go to node 2 too, eventhough 1 and 2 are separate SCCs. QED! :)
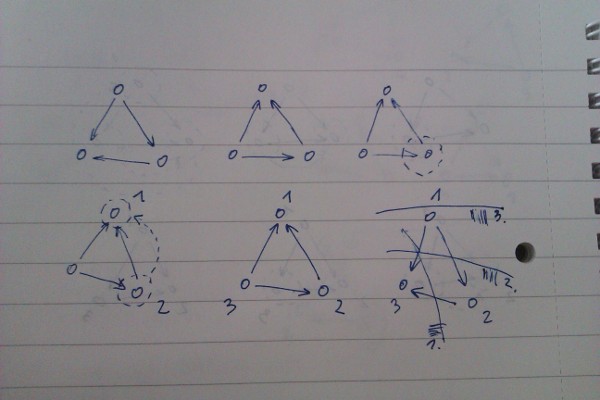
The last cartoon is an example of how correct implementation of the algorithm will find correct SCCs even for this modified situation.
Previous:
Improving the quality of large legacy codebase by incrementally enforcing encapsulation
Next:
My view of Coursera and Algorithms: Design and Analysis course